Symmetrization

In mathematics, symmetrization is a process that converts any function in n variables to a symmetric function in n variables. Conversely, anti-symmetrization converts any function in n variables into an antisymmetric function.

1 2 variables
- 1.1 Bilinear forms
- 1.2 Representation theory
2 n variables
3 Bootstrapping
4 Notes
5 References

2 variables

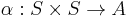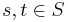Let $S$ be a set and $A$ an Abelian group. Given a map $\alpha: S \times S \to A$ , $\alpha$ is termed a symmetric map if $\alpha(s,t) = \alpha(t,s)$ for all $s,t \in S$ .

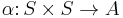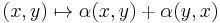The symmetrization of a map $\alpha \colon S \times S \to A$ is the map $(x,y) \mapsto \alpha(x,y) %2B \alpha(y,x)$ .

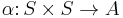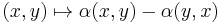Conversely, the anti-symmetrization or skew-symmetrization of a map $\alpha \colon S \times S \to A$ is the map $(x,y) \mapsto \alpha(x,y) - \alpha(y,x)$ .

The sum of the symmetrization and the anti-symmetrization is 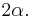$2\alpha.$ Thus, away from 2, meaning if 2 is invertible, such as for the real numbers, one can divide by 2 and express every function as a sum of a symmetric function and an anti-symmetric function.

The symmetrization of a symmetric map is simply its double, while the symmetrization of an alternating map is zero; similarly, the anti-symmetrization of a symmetric map is zero, while the anti-symmetrization of an anti-symmetric map is its double.

Bilinear forms

The symmetrization and anti-symmetrization of a bilinear map are bilinear; thus away from 2, every bilinear form is a sum of a symmetric form and a skew-symmetric form, and there is no difference between a symmetric form and a quadratic form.

At 2, not every form can be decomposed into a symmetric form and a skew-symmetric form – for instance, over the integers, the associated symmetric form (over the rationals) may take half-integer values, while over 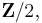$\mathbf{Z}/2,$ a function is skew-symmetric if and only if it is symmetric (as $1=-1$ ).

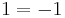This leads to the notion of ε-quadratic forms and ε-symmetric forms.

Representation theory

In terms of representation theory:

exchanging variables gives a representation of the symmetric group on the space of functions in two variables,
the symmetric and anti-symmetric functions are the subrepresentations corresponding to the trivial representation and the sign representation, and
symmetrization and anti-symmetrization map a function into these subrepresentations – if one divides by 2, these yield projection maps.

As the symmetric group of order two equals the cyclic group of order two (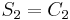 $S_2=C_2$ ), this corresponds to the discrete Fourier transform of order two.

n variables

More generally, given a function in n variables, one can symmetrize by taking the sum over all 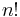$n!$ permutations of the variables^[1], or anti-symmetrize by taking the sum over all 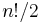$n!/2$ even permutations and subtracting the sum over all 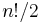$n!/2$ odd permutations.

Here symmetrizing (respectively anti-symmetrizing) a symmetric (respectively anti-symmetric) function multiplies by n! – thus if n! is invertible, such as if one is working over the rationals or over a field of characteristic $p > n,$ then these yield projections.

In terms of representation theory, these only yield the subrepresentations corresponding to the trivial and sign representation, but for 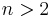$n > 2$ there are others – see representation theory of the symmetric group and symmetric polynomials.

Bootstrapping

Given a function in k variables, one can obtain a symmetric function in n variables by taking the sum over k element subsets of the variables. In statistics, this is referred to as bootstrapping, and the associated statistics are called U-statistics.

Notes

^ Hazewinkel (1990), p. 344

References

Hazewinkel, Michiel (1990). Encyclopaedia of mathematics: an updated and annotated translation of the Soviet "Mathematical encyclopaedia". Encyclopaedia of Mathematics. 6. Springer. ISBN 978-1-55608-005-0. http://www.springer.com/mathematics/book/978-1-55608-005-0?cm_mmc=Google-_-Book%20Search-_-Springer-_-0.